Using Self-Attention Attributions to Explain Transformers that Learned Chess

December 6, 2024

Introduction

Saliency maps are widely used to explain deep learning models by highlighting which parts of the input contribute most to a model's prediction. This study examines gradient-based saliency maps—particularly Self-Attention Attribution—in the context of transformers trained on chess. The state of the art chess engines are very powerful due to how they leverage a search algorithm to consider the the best paths a game could take. However, Ruoss and others where able to train a transformer model to near gradmaster level without using any explict searching to evaluate future moves [1], which makes their model quite impressive.

A neural network carrying out the complex task of evaluating a chessboard to the level of search based chess engines could imply that the information within the layers of the network must be uncovering some deeper insight in the position. Therefore, in this project we aim to use saliency maps to expose that deeper insight hidden within the model. In this project we produced saliency maps the following ways:

  • Integrated Gradients: State of the art saliency map generator, uses computed gradients from the model, focuses on the importance of the inputed values.
  • Raw Attention: Uses the computed raw attention from a intermedary layer of the model.
  • Self-Attention Attribution: Uses Integrated Gradients to figure out the importance of the raw attention from a intermedary layer of the model.

We hypothesize that attention mechanisms allow transformers to approximate the decision-making of chess engines. We:

  • Train a 9M parameter encoder-only transformer on a chess dataset.
  • Implement Self-Attention Attribution to create saliency maps.
  • Compare them with Integrated Gradients and raw attention weights.
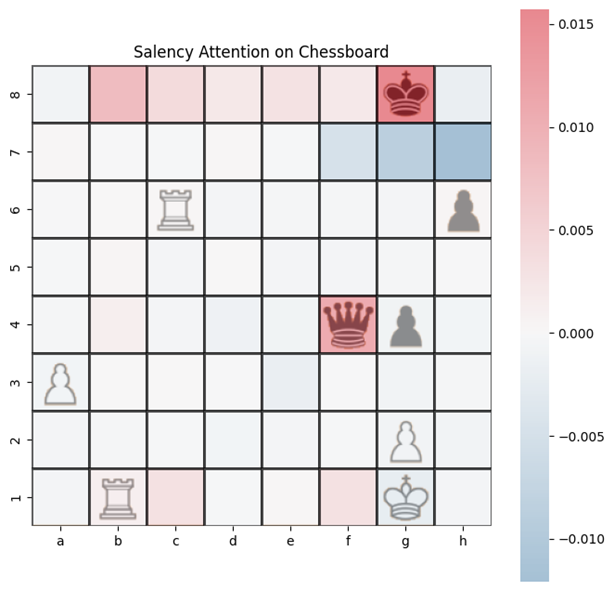
Theory Overview

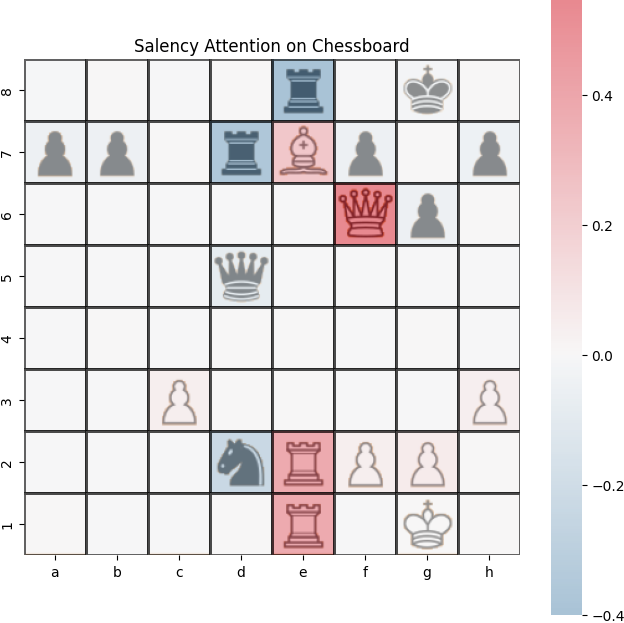
Example saliency map generated from our trained transformer model using Self-Attention Attribution.

Project Contributions

  1. Emprical evidence to show Self-Attention Attribution (AttAttr) in
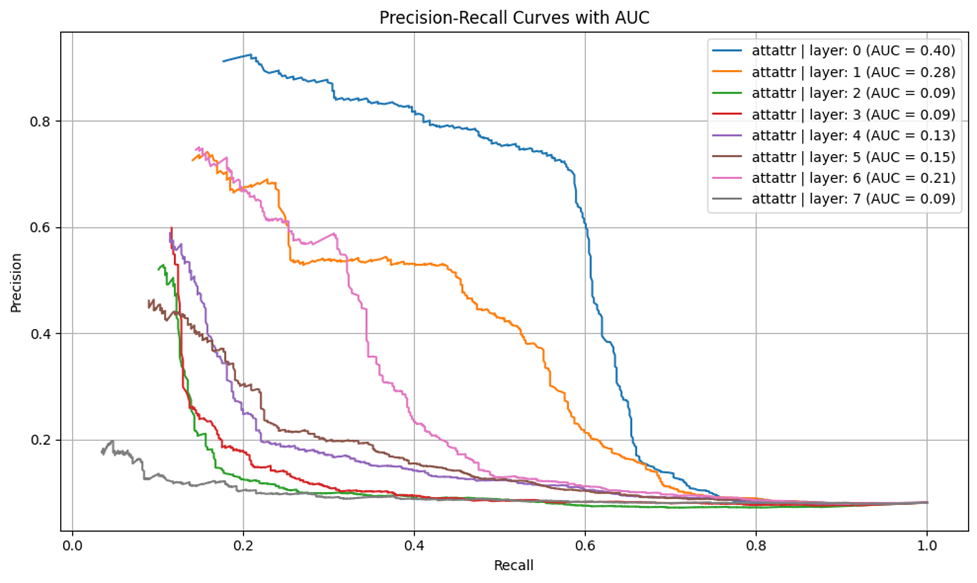
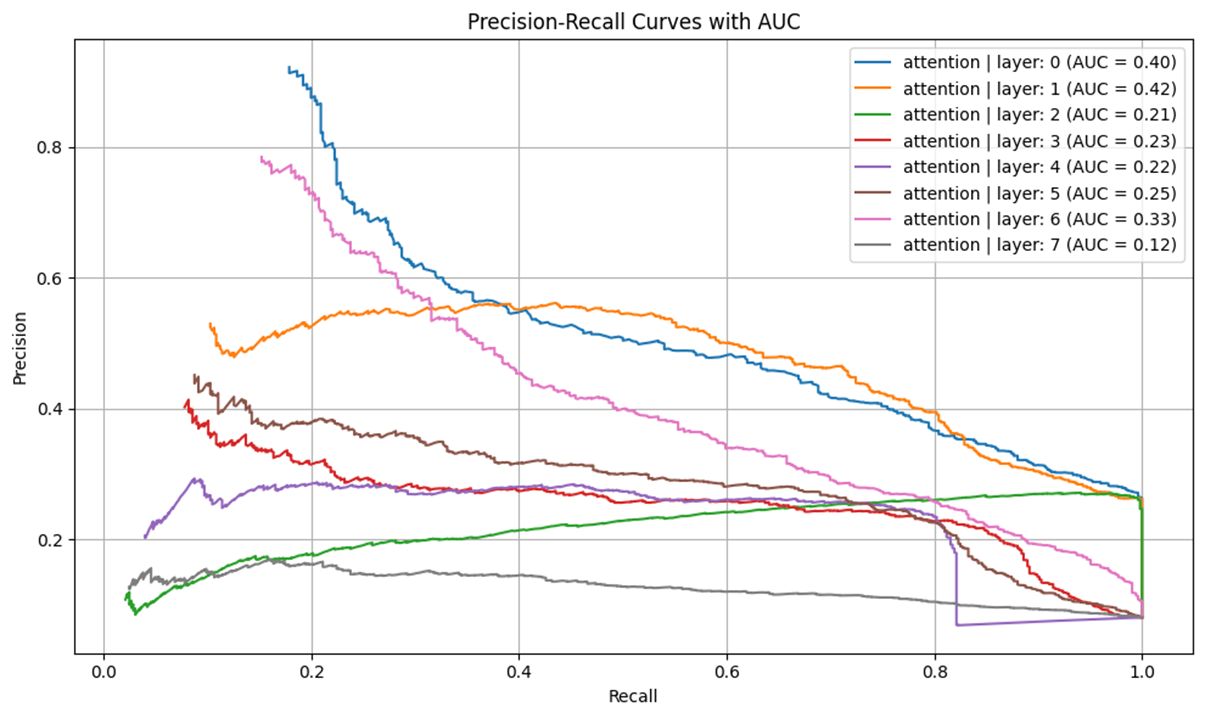
  2. Shallower layers provide easier to enterpret saliency maps than deeper layers.
  3. AttAttr maps outperform Integrated Gradients and raw attention-based maps.

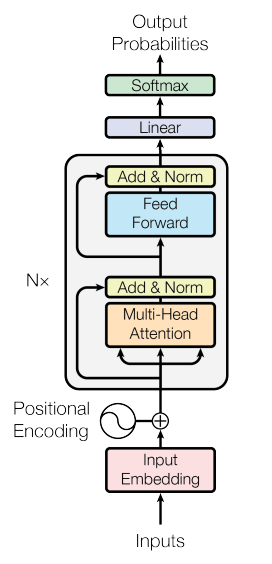
Transformer Architecture

Transformers process sequences using self-attention. Key components:

  • Embedding input tokens
  • Multi-head self-attention with queries, keys, and values
  • Final output logits for classification via softmax

We adapt the 9M parameter model from Ruoss et al. (2024) with these key changes:

  • Encoder-only design for better interpretability
  • 8 layers, 8 heads, 256 embedding dim
  • Output: 128 binned win probabilities
  • Improvements from LLaMA/LLaMA 2 (post-norm, SwiGLU)
Transformer Diagram

Gradient-Based Attribution Methods

Gradient-based attribution methods quantify how much each input feature contributes to the model’s prediction by analyzing the gradients of the output with respect to the inputs or internal components (e.g., attention weights). These methods provide insight into the model's decision-making process by highlighting which components most influence the output.

Integrated Gradients

Integrated Gradients is a path-based attribution method introduced to address issues with standard gradient methods, such as saturation and local non-linearity. Instead of computing the gradient at a single input point, Integrated Gradients averages gradients taken along a straight-line path from a baseline input to the actual input.

Let xx be the input, and x′x' a baseline input (e.g., a zero vector). The attribution for feature ii is computed as:

IGi(x)=(xi−xi′)⋅∫α=01∂F(x′+α(x−x′))∂xidα\text{IG}_i(x) = (x_i - x'_i) \cdot \int_{\alpha=0}^1 \frac{\partial F(x' + \alpha (x - x'))}{\partial x_i} d\alpha

This formulation ensures that attributions satisfy desirable properties like completeness (the attributions sum to the output difference) and sensitivity (if changing a feature changes the prediction, it gets non-zero attribution).

In practice, the integral is approximated using a Riemann sum with mm steps:

IGi(x)≈(xi−xi′)⋅1m∑k=1m∂F(x′+km(x−x′))∂xi\text{IG}_i(x) \approx (x_i - x'_i) \cdot \frac{1}{m} \sum_{k=1}^{m} \frac{\partial F(x' + \frac{k}{m} (x - x'))}{\partial x_i}

Integrated Gradients is especially useful in vision and NLP applications where baselines are meaningful (e.g., black images or padding tokens).

Self-Attention Attribution (AttAttr)

AttAttr explains which attention connections are influential by computing a path integral of the gradients with respect to the attention weights.

To extract the latent information from each attention head AhA_h in layer hh in the transformer, we can utilize Self-Attention Attribution [^hao2021]. Self-Attention Attribution can be expressed as computing a line integral from 00 to AA of the partial derivative ∂F∂Ah\frac{\partial F}{\partial A_h}, as seen in the equation below:

A=[A1,…,A∣h∣]A = [A_1, \ldots, A_{|h|}]
AttAttrh(A)=Ah⊙∫α=01∂F(αA)∂Ah∈Rn×n\text{AttAttr}_h(A) = A_h \odot \int_{\alpha=0}^1 \frac{\partial F(\alpha A)}{\partial A_h} \in \mathbb{R}^{n \times n}

Here, ⊙\odot denotes element-wise multiplication. Ah∈Rn×nA_h \in \mathbb{R}^{n \times n} represents the hh-th head's attention weight matrix. The output AttAttrh(A)\text{AttAttr}_h(A) denotes which attention connections in the attention weight are most important:

  • Positive connections increase the output of the function FF
  • Negative connections decrease the output
  • Connections close to 00 are considered not important

Self-Attention Attribution can be efficiently computed using a Riemann approximation of the integral. In other words, sum the gradients at mm evenly spaced intervals along the path:

Attrh(A)=Ahm⊙∑k=1m∂F(kmA)∂Ah\text{Attr}_h(A) = \frac{A_h}{m} \odot \sum_{k=1}^m \frac{\partial F\left(\frac{k}{m} A\right)}{\partial A_h}

[^hao2021]: Hao, J., Ren, H., & Chen, H. (2021). Self-Attention Attribution: Interpreting Information Interactions Inside Transformer. arXiv preprint arXiv:2104.05274.

[^hao2021]: Hao, et al. Self-Attention Attribution: Interpreting Information Interactions Inside Transformer. 2021.

Dataset

  • Training: 10M games from Lichess → 15.3B state-action pairs
  • Testing: 1K games (~1.8M pairs), 14.7% overlap with training

FEN Tokenization:

  • Convert FEN board state: replace digits with '.', remove '/'
  • Treat each character as a token

FEN Tokenization

Evaluation Metrics

  • Action Accuracy: Picks correct move
  • Kendall's Tau: Correlation with Stockfish rankings
  • Puzzle Accuracy: Solves chess puzzles (ELO 299–2867)

Training Setup

  • 20% of an epoch, Adam (lr = 1e-4), batch size 4096, 180K steps
  • 6× NVIDIA A100 GPUs

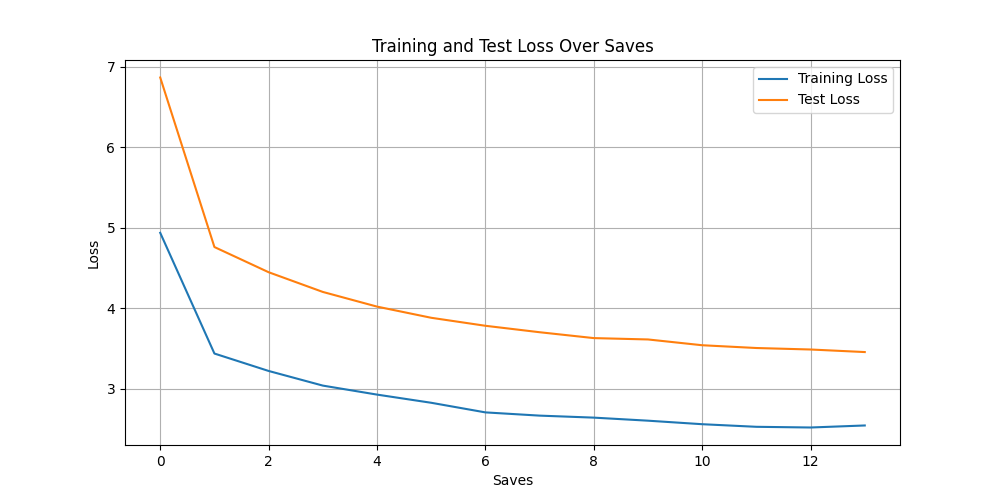
Training Loss

Results:

MetricEncoder (ours)Decoder (original)
Action Accuracy55.1%63.0%
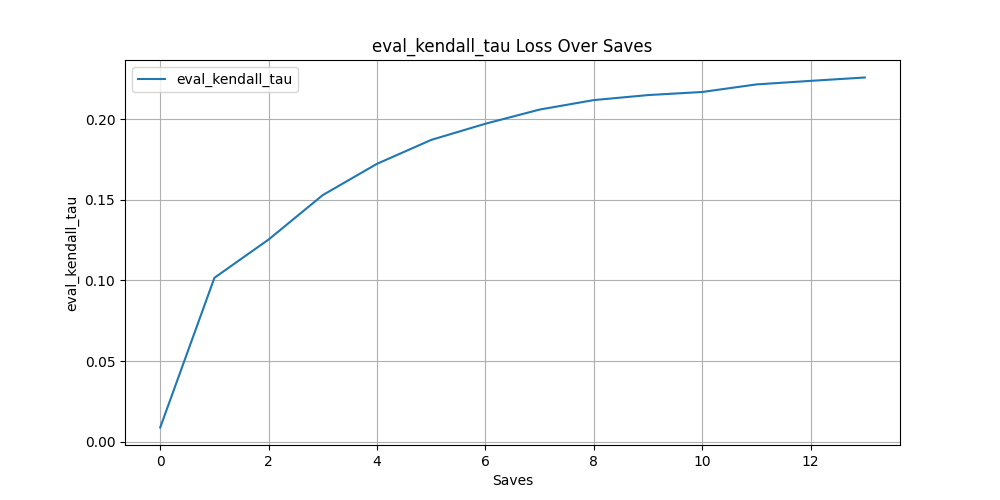
Kendall’s Tau0.22570.259
Puzzle Accuracy67.8%83.3%

Self-Attention Attribution Experiments

Saliency Map Generation

To reduce computation:

  1. Use only best move (remove M)
  2. Collapse output to expected win prob
  3. Aggregate attention across heads

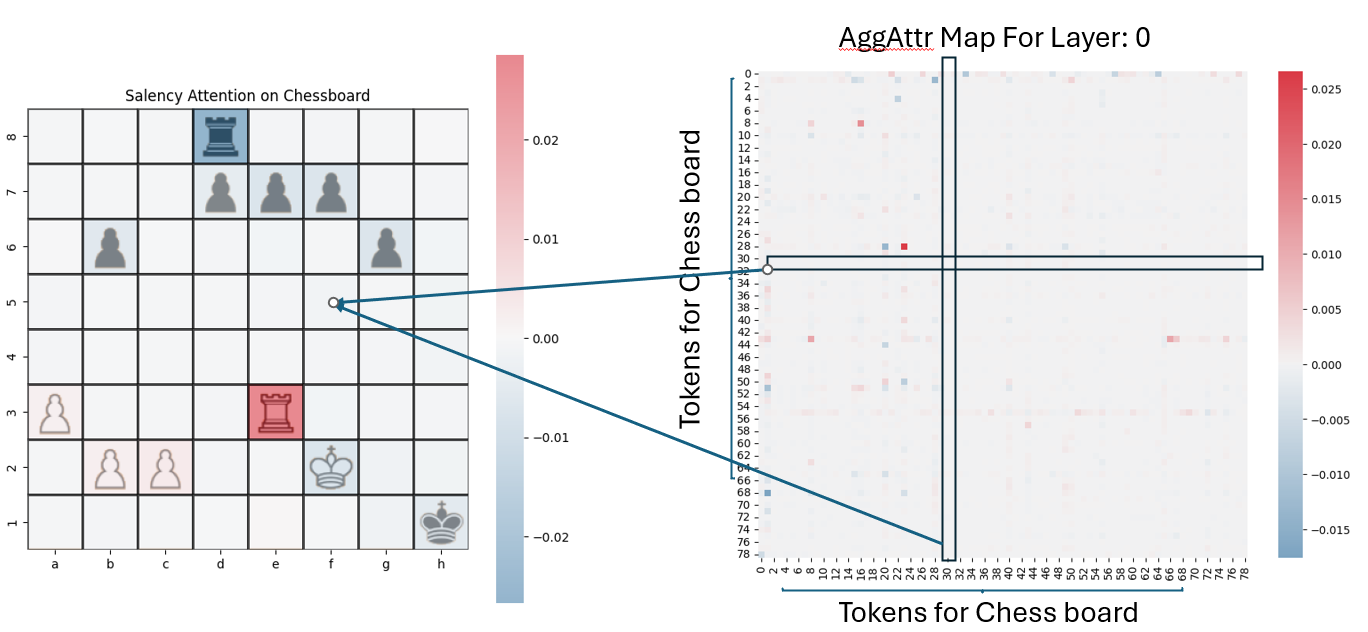
From the resulting attention attribution matrix, saliency per token is computed by summing attention to/from the token. Theory Overview

How To Compare Saliency Maps

Baseline Comparisons

  • Integrated Gradients (IG):
    • Input: raw embeddings of FEN
    • Baseline: empty board
  • Raw Attention Weights:
    • Aggregate attention weights across heads
    • Compute saliency per token as in AttAttr

Method Comparison

Evaluation Method

  • Use Chess Saliency Dataset (100 puzzles + human annotations)
  • Normalize maps (min-max), binarize with threshold
  • Compute precision and recall over thresholds

PRC - AttAttr
PRC - Attention

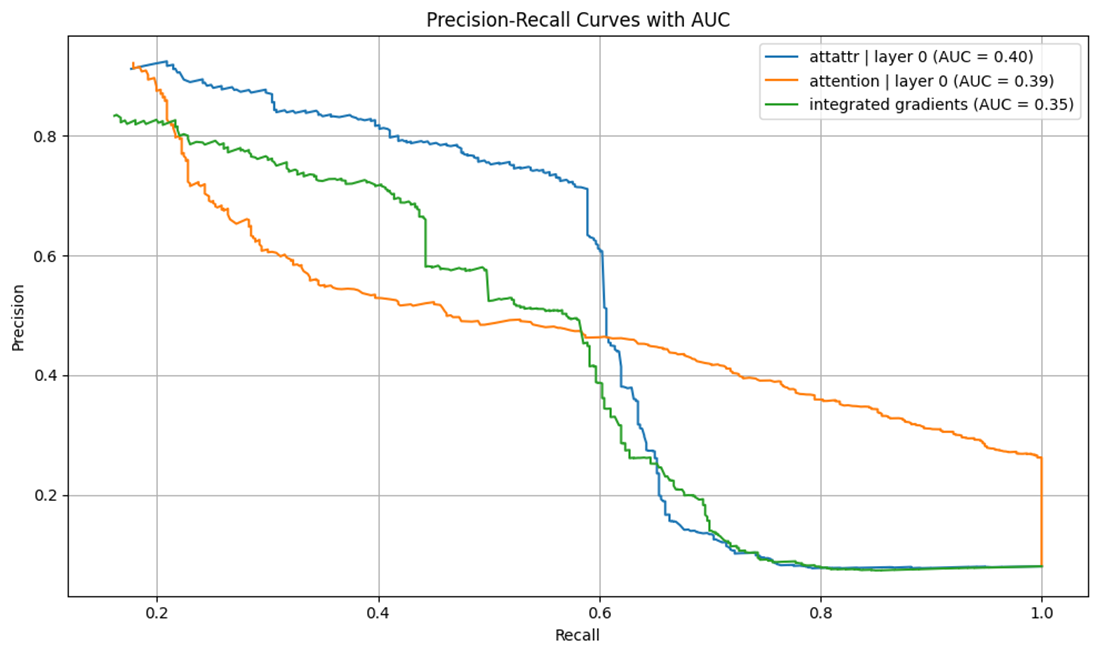
Results: Qualitative Examples

Visual maps show:

  • AttAttr (layer 0) matches ground truth well
  • IG and raw attention less precise
AttAttr Layer 0

AttAttr (Layer 0)

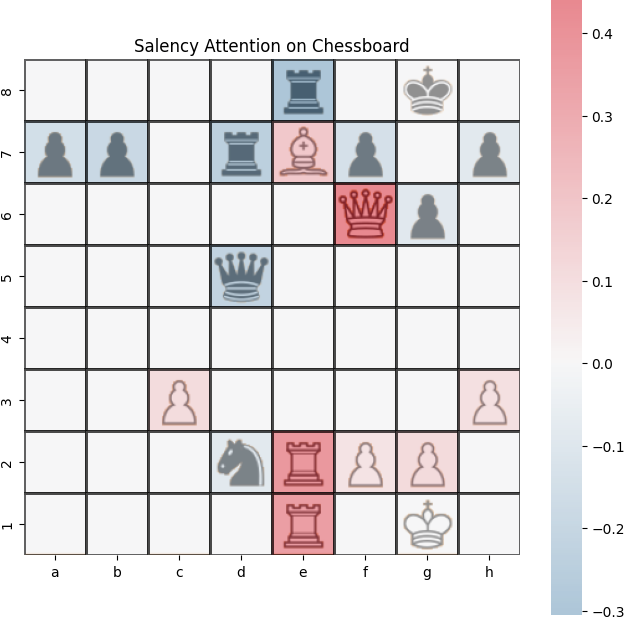
Integrated Gradients

Integrated Gradients

Quantitative Analysis

  • 1: Layer 0 AttAttr has non-trivial AUC (>0.15)
  • 2: Shallower layers outperform deeper ones (see Figure 6)
  • 3: AttAttr consistently outperforms IG and raw attention maps

Kendall's Tau

Interpretation

While deeper layers underperform on saliency benchmarks, they may encode other types of strategic reasoning. Example: layer 8 highlights empty squares on rank 8—a useful concept in chess not captured by the saliency dataset.

Conclusion

This study demonstrates that:

  • Self-Attention Attribution can produce interpretable saliency maps
  • Shallower transformer layers yield the most informative saliency
  • These maps outperform standard methods like IG and raw attention

Future work could explore deeper layers with advanced hypothesis testing to understand their strategic role in model reasoning.

Play Chess Against My Model

Try playing against the AI:

References

[1]: Hao et al. (2021). Self-Attention Attribution.

[2]: Puri et al. (2020). Chess Saliency Dataset.

[3]: Ruoss et al. (2024). Amortized Planning with Large-Scale Transformers.

[4]: Sundararajan et al. (2017). Integrated Gradients.

[5]: Vaswani et al. (2023). Attention is All You Need.